FHE
Fully homomorphic encryption
Introduction
The blog post tries to explain the idea of fully homomorphic encryption, Consider two messages $m1,\ m2$ being stored in a public cloud or a datacenter. Let the encrypted ciphertext which are stored there be $c1 = enc_k(m1), c2 = enc_k(m2)$, and now if we have to perform an operation(say concat these messages), we need to decrypt the entire message m1 and m2 and encrypt them again at store, there is a possibilty of plaintext leakage during this operation.

FHE allows you to calculate the encrypted ciphertext say $c’$ without needing to decrypt $m1, \ m2$, Hence for the operator $\oplus$
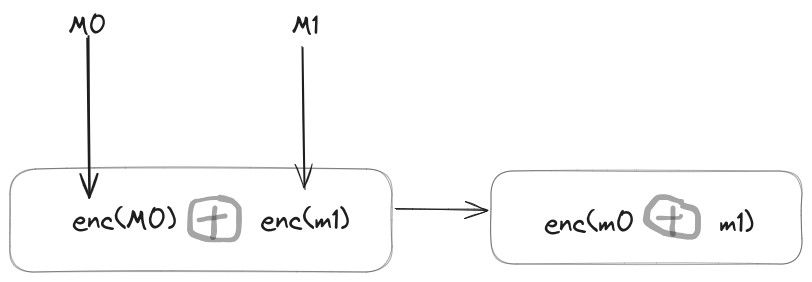
$$\begin{align*} \text{enc}{\text{pk}}(m_1)\ {\oplus}\ \text{enc}{\text{pk}}(m_2) &= \text{enc}{\text{pk}}(m_1\ {+}\ m_2) \end{align*}$$
In other words, FHE allows computations to be performed on a ciphertext without needing to decrypt it. Applications of FHE can be in block chain, cloud security and federal agencies/government orgs which needs to perform their own computations without compromising the privacy. Let’s start with an example.
Setup
Now we have gained some intro on FHE, let’s try to look at an example and deduce the computations. We will be going through an example from OpenFHE githubwhich is actively developed and supports schemes that include BGV, CKKS, BFV, FHEW, TFHE and CKKS bootstrapping
The setup doc is pretty much self-explanatory and would suggest this extension for debugging the binaries.
This is the only addition required in c_cpp_properties.json to get it running:
"includePath": [
"/usr/local/include/openfhe",
"${workspaceFolder}/**"
],
Let’s take the example of integer arithmetic homomorphic operations using BFV scheme:
BFV is constructed based on RLWE(Ring learning with errors) and operates on ciphertext and plaintext ring. It is computationally hard to solve even for quantum computers.
Data Representation:
The plaintext and ciphertext spaces are defined over two distinct polynomial rings where $ P \ = R_t $ and $ C \ = R_q \times R_q $ and $t, q \in \mathbb{Z} $.
There are several parameters required for the keygen and encryption of the BFV:
Key and Error distributions - $D1, D2$
Ring $R$ and modulus $q$
Integer modulus for the plaintext $P$
Before encrypting the message $m$, we need to turn it into a polynomial, for example if we want to encrypt $(5(101))$, the representation would be $1 * x^2 + 0 * x^1 + 1 = x^2 + 1$
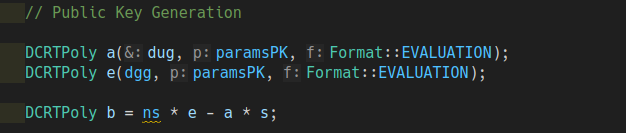
Key generation:
Generating this private key is straightforward. We essentially use random small coefficients from the distribution $D1$,
The public key consists of two elements $A$ and $t$. $A$ is a random polynomial from the distribution $D1$ and for computing $t$ we need to do a matrix operation:
$$ \begin{aligned} t = As + e \end{aligned} $$
where $e$ is the small error vector from the distribution d2.
Secret key: $s$
Public key: $(t, A)$
Encryption:
Encrypt($m$):
Randomly choose: $ u \leftarrow D1 \ $
Randomly choose noise: $ e1, e2 \leftarrow D2 \ $

- Compute the ciphertext: $$ \begin{align} c[0] &= [pk[0] * u + e1 + \delta *m] * q, & \\ c[1] &= [pk[1] * u +e_{2}] * q \end{align} $$

The parameter $\delta $ is the quotient of $q \div t $, which is used to scale the message, these values can be modified as the part of generating cryptocontext.

Decryption:
Decrypt($c$):
- Compute:$\ $ $ tmp \ = [c[0]+c[1]*s]\ q $
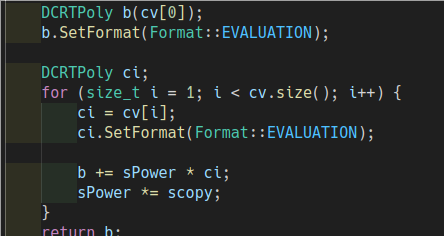
- Compute the message: $ m = (round(tmp*t/q))t $. t is used to calculate the congruence of $ x\ mod\ q $ in set $ \mathbb{Z} $

Proof of decryption:
$$ \begin{align} c[0] + c[1] \cdot s &= pk[0] \cdot u + e1 + \delta m + (pk[1] \cdot u + e2) \cdot s & \\ &= -(a \cdot s + e) \cdot u + e1 + \delta m + a \cdot u \cdot s + e2 \cdot sk \nonumber \\ &= -a \cdot u \cdot s - e \cdot u + e1 + \delta m + a \cdot u \cdot s + e2 \cdot s \nonumber \\ &= \delta m - e \cdot u + e1 + e2 \cdot s \nonumber \\ &= \delta m + v \nonumber \end{align} $$
where $s, e1, e2, sk$ are all small vectors.